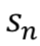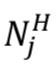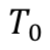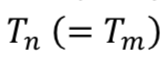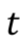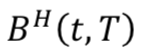Pricing Cross-Currency Swaps

Let's consider a cross-currency swap (CCS) paying a fixed rate in a home currency and receiving an IBOR floating rate in a foreign currency.

In this swap, we:

• Pay  at the dates 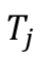 (with )
• Receive 

The valorization of the home currency leg is the same as in the vanilla swap but we have to include the nominal difference at each payment date since we do not pay in the same currency:

For the foreign currency leg, the forward rates are calculated in a classic way using the zero coupon of the foreign currency (and the respective tenor):

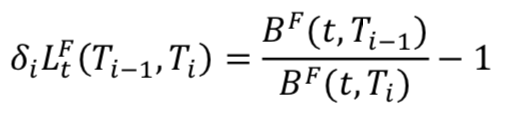
The discounting curve used to valorize the foreign currency leg is not the zero coupon discounting curve in the foreign currency but a zero coupon previously built from the basis CCS spreads between the two currencies. We call this curve .

The valorization of the foreign currency leg is:

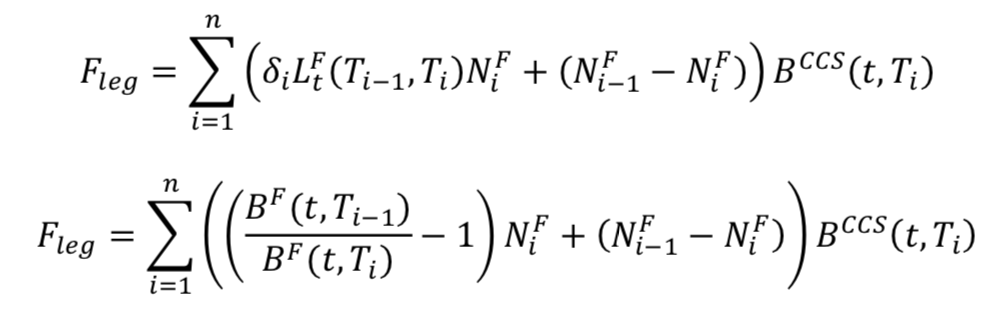
We calculate the valorization of the cross-currency swap with the FX spot rate between the two currencies at the market date :

Building Zero Coupon

A broker daily sends us the basis cross-currency swap spreads for different currency pairs.

There are different spreads for different swap maturities (from 1Y to 30Y, for example).

From the definition of the basis spread we have:

Here, the swaps start at the publication date, so .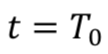

We can reverse the formula:

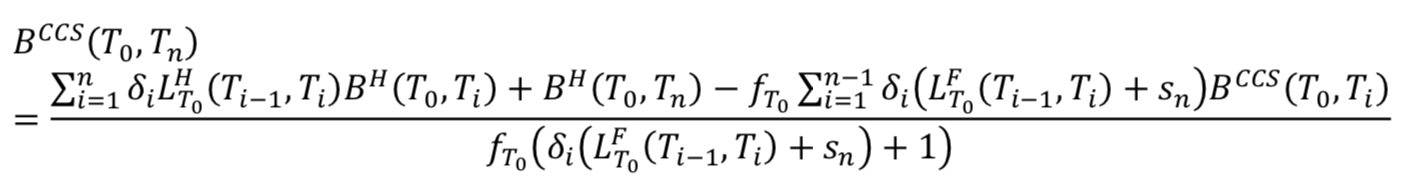
We can see that 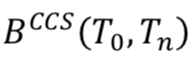 is a function of the previous  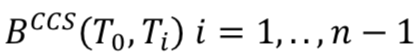and .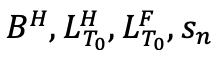

For the zero coupon, we can then build the CCS zero coupon curve with a bootstrapping method, starting from the first swap (1Y) and calculating 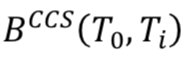 one after the other (of course, ).

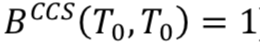To finish, we interpolate linearly between the values deduced from the bootstrapping method to get a curve defined on each point.